https://www.engraved.blog/why-machine-learning-algorithms-are-hard-to-tune/ https://www.engraved.blog/how-we-can-make-machine-learning-algorithms-tunable/
- liniowa kombinacja funkcji strat jest tak naprawdę wszędzie. Taką kombinacją są w istocie:
- regularyzacja L1 i L2 (i często robi się jej hiperoptymalizację!)
- funkcja straty w GANach - balans między funkcją straty generatora i dyskriminatora
- za pomocą tej liniowej kombinacji próbujemy zbalansować często przeciwne siły - nie wiemy w dodatku jak je poprawnie zbalansować, więc wprowadzmay hiperparametr - wagi - i próbujemy tę wagę optymalizować
Problem Model może zignorować jedną z funkcji strat, optymalizując tylko tą drugą. Hiperoptymalizacja może nic nie pomóc, bo poniżej pewnej wartości parametru model ignoruje jedną funkcję straty, a powyżej ignoruje drugą funkcję straty. Można zastosować early stopping, ale to tylko ukrywa problem, a go nie rozwiązuje ani go nie wyjaśnia.
Wyjaśnienie
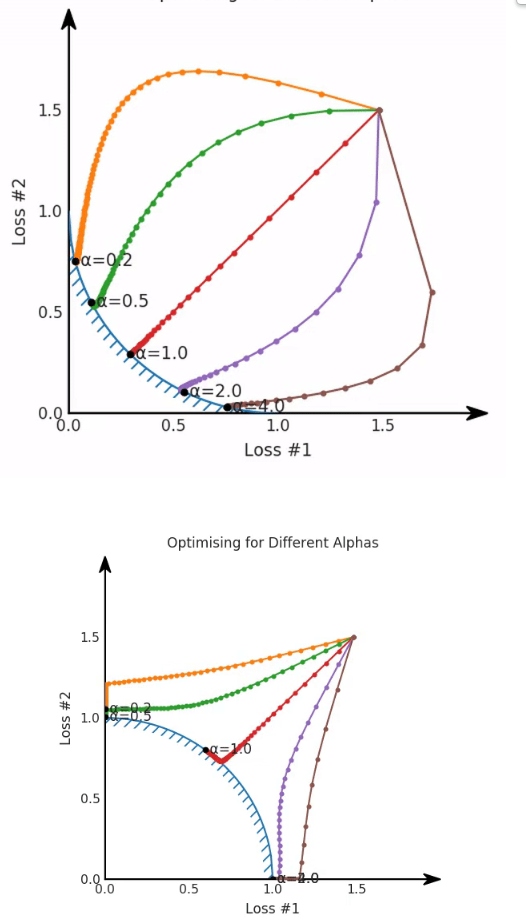
Żeby wyjaśnić problem trzeba patrzeć na krzywą Pareto (czyli zbiór wszystkich Rozwiązanie optymalne w sensie Pareto). Jeśli ta krzywa jest wypukła to model nauczy się ignorować jedną z funkcji strat. Na górze wklęsła, na dole wypukła:
Wnioski
- Suma dwóch loss’ów wcale nie musi dobrze balansować między nimi
- prawdziwa krzywa Pareto dla realnych problemów nie jest znana i w dodatku będzie składać się z wielu odcinkami wypukłych i wklęsłych części. Wtedy nigdy nie zatrzymamy się w wypukłych częściach krzywej Pareto, lądując zawsze w którejś w wklęsłych - a to, w której części się znajdziemy zależy od inicjalizacji:
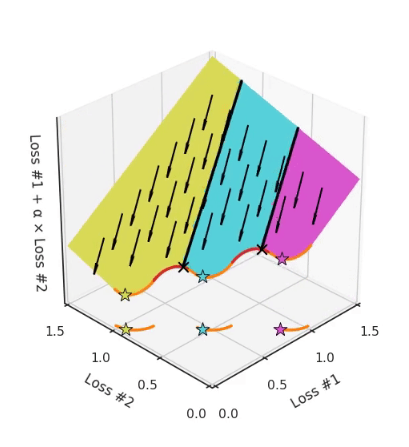
- najważniejsze wniosek: zmiana wag w funkcjach strat może mieć nieprzewidywalne konsekwencje
W drugim artykule podano optymalne rozwiązanie - wymaga mnożników Lagrange’a.