Embedding Binarization Problem

Problem polega na znalezieniu sposobu, który przerobi wektor dense (czyli z wartościami ze zbioru liczb rzeczywistych) na wektor binarny (tylko zera i jedynki), najlepiej w jakiś wyuczalny sposób. Bardziej formalnie jest to sposób na przejście z Euclidean Space do Hamming Space.

SUBIC zawiera zgrabne podsumowanie i porównanie kilku publikacji robiących supervised hashing: 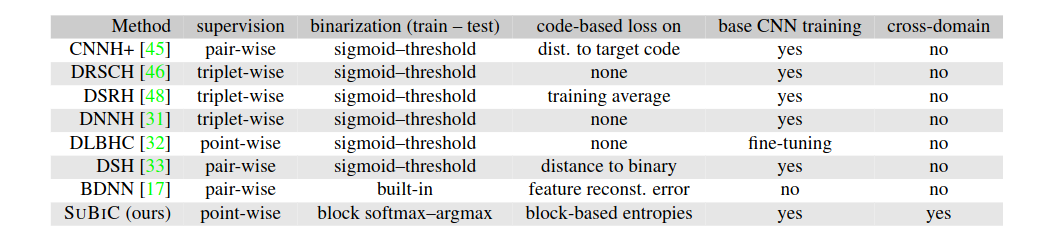Z powyższej tabeli i samej treści publikacji wynika, że wszystkie wymienione metody trenują w dwóch krokach - najpierw sieć która przewiduje wektor dense, potem zamrażają tą sieć, zamieniają na binary poprzez sigmoid-threshold i ostatnią warstwę uczą na wektorach binarnych już.

Learning-based hashing dzieli się na (źródło: Deep Hashing for Compact Binary Codes Learning):

1. unsupervised
   1. Mapowanie danych wejściowych na rozkład jednostajny nad przestrzenią sferyczną (tak robią w Spreading vectors for similarity search)
   2. LSH
2. semi-supervised
3. supervised
   1. DSH Główny pomysł do dodanie do lossa, który minimalizuje odległość elementy w wektorze dense do -1 lub +1, ale nie robią wcześniej sigmoida!
   2. Deep Hashing for Compact Binary Codes Learning Uwaga: bardziej teoretyczne podejście do prawie tego samego rozwiązania i modyfikacja maksymalizacji wariancji i maksymalizacji niezależności zaprezentowana w BDNN. Wektor binarny robią z wektora dense poprzez funkcję signum. Proponują loss składający się z kilku części:
      1. po prostu porównanie wektora binarnego z wektorem dense i minimalizacja różnicy
      2. maksymalizacja wariancji w wektorach binarnych
      3. maksymalizacja niezależności między poszczególnymi bitami
   3. SUBIC.
      1. Podstawowy pomysł to podzielenie wektora dense na bloki pewnej długości.
      2. Podczas treningu na każdy blok z osobna nakładany jest softmax; podczas testu każdy z bloków zamieniany jest na one-hot w taki sposób, że 1 pojawia się tam, gdzie wartość bloku po softmaxie (albo przed, to jest to samo) jest największa.
      3. Wymuszają, żeby wektor po softmaxie (czyli wektor dense) był jak najbliżej binarnemu poprzez dodanie do lossa entropii - minimalizując entropię chcemy, żeby wektor po softmaxie był bliski temu po one-hot, tzn. tylko w jednym miejscu miał 1

Pomysły

1. żeby uniknąć problemów z brakiem gradientu można mieć dwie warstwy które przewidują wyjście, tzn. raz przewidywac p-stwo klika z warstwy dense, potem zrobić fikołek binaryzujący i drugi raz przewidywać o-stwo klika z takiego binarnego stworzenia. Tylko że to chyba też nie będzie uczyło się produkować dobrych wektorów do robienia thresholdu, no bo nie będzie można policzyć gradientu z binary do reszty sieci?##https://www.cv-foundation.org/openaccess/content_cvpr_2015/papers/Liong_Deep_Hashing_for_2015_CVPR_paper.pdf
2. można zastosować LSH zamiast zwykłych wyuczalnych thresholdów, będzie to na pewno elastyczniejsze tu pomysł jak to klepnąć: Implementing LSH Functions in Tensorflow
3. sigmoid threshold może być wyuczalny! ← można go chyba osiągnąć poprzez przemnożenie przez warstwę liniową
4. można zastosować Entropia binarna i porównać z obecnym rozwiązaniem
5. przeczytać related work w https://www.cv-foundation.org/openaccess/content_cvpr_2015/papers/Liong_Deep_Hashing_for_2015_CVPR_paper.pdf

Wyniki

hashes	inne	test pc48h BSS	test lc120h BSS	val lc120h BSS	train lc120h BSS	best epoch	link
-	-	0.0333	0.0153	0.0177	0.0207	7	(baseline)
128	-	0.0241	0.0101	0.0127	0.0144	~80	click
512	-	0.0264	0.0106	0.0143	0.0187	15	click
2048	-	0.0279	0.0121	0.0158	0.0215	11	click
2048	kernel l2 = 1e-5	0.0270	0.0119	0.0150	0.0210	11	click
2048	kernel l1 = 1e-5	0.0284	0.0130	0.0155	0.208	14	click
2048	kernel l1 = 1e-4	0.0306	0.0139	0.0163	0.0202	23	click
2048	kernel l1 = 1e-3	0.0293	0.0126	0.0156	0.0166	11	click
2048	kernel l1 = 1e-4, no bias	0.0309	0.0139	0.0165	0.0202	22	click
4096	-	0.0265	0.0132	0.0141	0.0233	8	click
4096	kernel l2 = 1e-5	0.0265	0.0128	0.0140	0.0210	7	click
4096	kernel l1 = 1e-4, no bias	0.0304	0.0140	0.0164	0.0195	7	click

Wyniki CTR

hashes	inne	test BSS	val BSS	train BSS	level of bin	link
-	-	0.0357	0.0372	0.0432	-	(baseline)
4096	-	0.0325	0.0341	0.0421	-	click
8192	-	0.0325	0.0345	0.0440	-	click
-	learnable bin, no extra loss	0.0356 / 0	0.0368 / 0	0.0446 / 0	0.26 / 1	click
-	learnable bin, loss weight=0.1	0.0364 / 0	0.0374 / 0	0.0440 / 0	0.81 / 1	click
-	learnable bin, loss weight adaptive from 0.1 to $\inf$	0.03605 / 0			0.82 / 1	click
4096	probit				-	click
4096	probit, extra dense layer	0.0309	0.0321	0.0390	-	click