Transformer w czystej formie nie ma żadnej informacji o położeniu elementów sekwencji, nie wie czy dane słowo/wartość jest na początku czy na końcu zdania/sekwencji (źródło: Transformers in Time-series Analysis A Tutorial).
Positional Encoding ma naprawić ten problem, czyli wprowadzić informację o położeniu słowa, ale co ważniejsze, wprowadzić też informację o położeniu dwóch słów względem siebie.
sin-cos positional encoding
Oryginalnie zaproponowane w Attention Is All You Need. Tego typu Positional Encoding jest zaprojektowany tak, że jeśli słowa są oddalone od siebie o stałą odległość, to ich positional embeddingi będą takie same z dokładnością do takiego samego przekształcenia liniowego (źródło: Transformers in Time-series Analysis A Tutorial, Transformer Architecture The Positional Encoding).
O sin-cos positional encoding można myśleć jak o ciągłej wersji enkodowania binarnego liczb, tzn. chcąc zamienić liczby od 0 do 8 w embedding o wymiarze moglibyśmy zakodować te liczby po prostu binarnie:
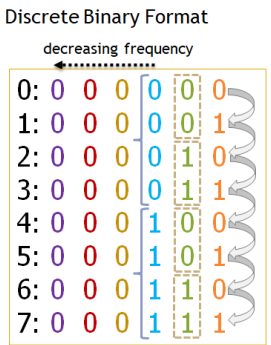 Zwróćmy uwagę, że częstotliwość zmian między 0 a 1 jest różna dla różnych kolumn (maleje idąc od prawej do lewej strony).
Zwróćmy uwagę, że częstotliwość zmian między 0 a 1 jest różna dla różnych kolumn (maleje idąc od prawej do lewej strony).
Możemy przejść z binarnej wersji takiego kodowanie do ciągłej używając właśnie sinusów i cosinusów, tzn. zamiast naprzemiennie występujących wartości 0 i 1 występują liczby rzeczywiste “płynnie” zmieniające się między -1 a 1, z coraz to mniejszą częstotliwością:
 Źródło: Transformers in Time-series Analysis A Tutorial.
Źródło: Transformers in Time-series Analysis A Tutorial.
Wizualnie można to przedstawić tak:
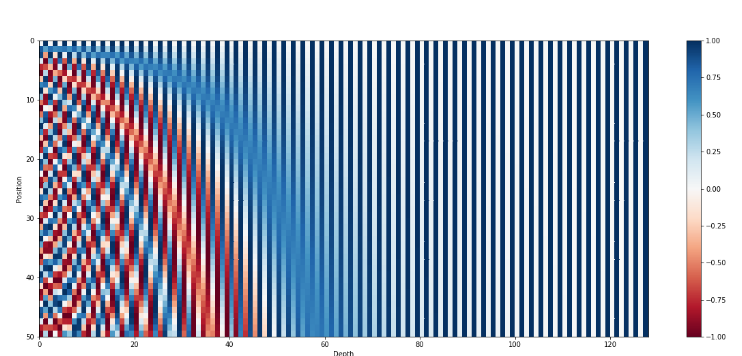 Źródło: Transformer Architecture The Positional Encoding
Źródło: Transformer Architecture The Positional Encoding
Positional encoding jest dodawane do embeddingów słów. Dlaczego to nie niszczy informacji zawartej w embeddingach słów? Dlatego, że największ zmienność w position encoding występuje w początkowych elementach wektora z embeddingiem, więc sieć może się nauczyć wypychać istotne informacje dla słów poza początkowe elementy. Źródło: Transformer Architecture The Positional Encoding.