Paradoks Simpsona
(w testach A/B i nie tylko)
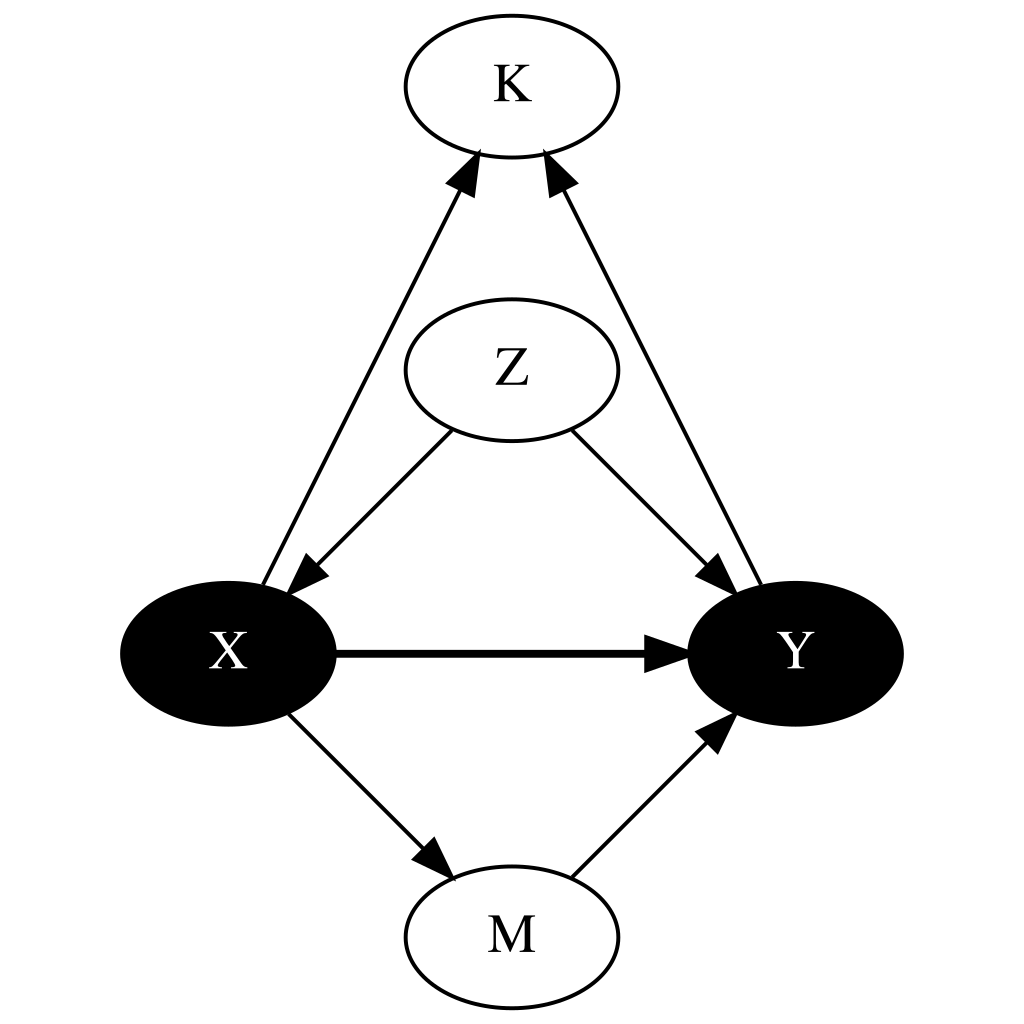
Graf przyczynowy i zmienna zakłócająca
 note:
note:
X - posiadanie parasola Y - mokre ubranie Z - padający deszcz
Przykład 1
::: block
Wyniki badania dotyczące odsetka zawałów w zależności od przyjmowania leku. Pacjenci sami decydowali czy brać lekarstwo.
| kobiety | mężczyźni | ogółem | |
|---|---|---|---|
| grupa kontrolna | |||
| grupa przyjmująca lekarstwo |
Paradoks Simpsona: Dlaczego jeśli u kobiet jest lepiej i u mężczyzn jest lepiej to ogółem jest gorzej?
Ponieważ:
\frac{A+C}{B+D} < \frac{a+c}{b+d}$$ <!-- element class="fragment" data-fragment-index="1" --> Kluczowe pytanie:<b> to jest w końcu lepiej lepiej czy gorzej?</b> <!-- element class="fragment" data-fragment-index="2" --> --- #### Przykład 2 ::: block <!-- element style="font-size:23px" align="center"--> Teraz weźmy inne badanie, w którym ludzi brali lek na obniżenie ciśnienia krwi. Po zakończeniu badania zastanawiano się czy lek wpływa również zmniejszenie odsetka zawałów. | | osoby z niskim ciśnieniem krwi | osoby z wysokim ciśnieniem krwi | ogółem | | --------------------------- | ------------------------------ | ------------------------------- | -------------------- | | grupa kontrolna | $\frac{1}{20} = 5\%$ | $\frac{12}{40} = 30\%$ | $\frac{13}{60}=22\%$ | | grupa przyjmująca lekarstwo | $\frac{3}{40} = 7.5\%$ | $\frac{8}{20}=40\%$ | $\frac{11}{60}=18\%$ | Kluczowe pytanie:<b> to jest w końcu lepiej lepiej czy gorzej?</b> <!-- element class="fragment" data-fragment-index="1" --> --- ##### Czym różnią się oba przykłady? ::: block <!-- element style="font-size:23px" align="left"--> **Przykład 1**. Wyniki badania dotyczące odsetka zawałów w zależności od przyjmowania leku. Pacjenci sami decydowali czy brać lekarstwo. Podział ze względu na płeć. ::: ```mermaid flowchart LR lekarstwo --> zawał płeć --> lekarstwo płeć --> zawał ``` ::: block <!-- element style="font-size:23px" --> <i><b>płeć</b> jest zmienną zakłócającą - patrzymy na odseparowane dane</i> ::: block <!-- element style="font-size:23px" align="left"--> **Przykład 2.** Ludzie brali lek na obniżenie ciśnienia krwi. Po zakończeniu badania zastanawiano się czy lek wpływa na zmniejszenie odsetka zawałów. ::: ```mermaid flowchart LR ciśnienie --> zawał lekarstwo --> zawał lekarstwo --> ciśnienie ``` ::: block <!-- element style="font-size:23px" --> <i><b>ciśnienie</b> jest pośrednikiem - patrzymy na dane łączne</i> --- #### Przykład testu A/B ::: block <!-- element style="font-size:23px" align="left"--> | | tydzień 1 | tydzień 2 | łącznie | | --------- | ------------------------ | ---------------------- | --------------------- | | wariant A | $\frac{70}{80} = 87.5\%$ | $\frac{10}{20} = 50\%$ | $\frac{80}{100}=80\%$ | | wariant B | $\frac{20}{20} = 100\%$ | $\frac{50}{80}=62.5\%$ | $\frac{70}{100}=70\%$ | Simpson? To znowu ty? Co się stało? Zmieniliśmy proporcje wariantów. ::: ```mermaid flowchart LR tydzień --> klikalność tydzień --> wariant wariant --> klikalność ``` notes: Jak to możliwe? Otóż w tygodniu 1 większość ruchu było w wariancie A, w tygodniu 2 większość ruchu była w wariancie B. Ze względu na gorszą globalnie klikalność w tygodniu 2 mamy zaburzone łączne wyniki. --- ##### Wnioski ::: block <!-- element style="font-size:23px" align="left"--> 1. Powinniśmy w takim przypadku zawsze patrzeć na odseparowane dane, a nie na łączne. 2. W czasie trwania testu A/B nie zmieniamy proporcji wariantów. A jeśli zmieniamy to zawsze restartujemy test. Podczas trwania testu można zmieniać procent ruchu jaki idzie to testu jako całość, ale nie można zmieniać proporcji ruchu pomiędzy wariantami. --- ::: block <!-- element style="font-size:23px" align="left"--> Źródła: 1. **The book of why**, Judea Pearl and Dana Mackenzie 2. [Software Testing Paradoxes, Microsoft](https://learn.microsoft.com/en-us/archive/msdn-magazine/2005/december/test-run-software-testing-paradoxes)