Bayesian Network

Inna nazwa to Belief Network, Causal Network. Źródło: Factor graphs and the sum-product algorithm.

Niezależność w grafie (źródło: CS 228 - Probabilistic Graphical Models)

Oznaczenie: jeśli X i Y są niezależne to piszemy $X ⊥ Y$ . Typy niezależności:

Common parent:
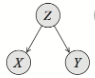Jeśli $Z$ jest zaobserwowany to $X ⊥ Y ∣ Z$ . Jeśli Z nie jest zaobserwowany to $X \neq ⊥ Y$ .
Cascade:
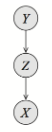Jeśli $Z$ jest zaobserwowany to $X ⊥ Y ∣ Z$ . Jeśli nie jest zaobserwowany to $X \neq ⊥ Y$ .
V-structure:
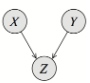Jeśli Z jest zaobserwowany to $X \neq ⊥ Y ∣ Z$ . Jeśli nie jest zaobserwowany to $X ⊥ Y$ . Przykład: Z to “czy trawnik jest mokry”, X to “padał deszcz”, Y to “podlewałem”. Jeśli trawnik w istocie jest mokry, czyli znamy Z to możemy wnioskować o X na podstawie Y, np. “nie podlewałem”, więc musiał padać deszcz!

Uwaga: powyższe 3 przypadki to są te same przypadki co w sieciach przyczynowych.

Ścieżka w grafie jest aktywna przy zaobserwowanych zmiennych $O$ jeśli dla każdej kolejnej trójki $X, Y, Z$ w tej scieżce zachodzi jeden z warunków:

X ← Y ← Z, gdzie $Y \neq \in O$
X → Y → Z, gdzie $Y \neq \in O$
X ← Y → Z, gdzie $Y \neq \in O$
X → Y ← Z, gdzie $Y \in O$ lub któryś z jego następców w grafie jest zaobserwowany

Zbiór wierzchołków $Q$ i $W$ w grafie są $d$ -separowalne przy zaobserwowanych zmiennych $O$ jeśli $Q$ i $W$ nie jest połączony żadną ścieżką aktywną.

Fakt: jeśli ” $p$ factorizes over $G$ ” oraz zmienne są niezależne w $G$ , to są również niezależne w $p$ . Twierdzenie odwrotne nie jest prawdziwe. Mówimy, że $G$ jest $I$ -map (independence map) dla $p$ .

Inference w Graphical Models (źródła: CS 228 - Probabilistic Graphical Models, A visual introduction to Gaussian Belief Propagation)

“Inference” oznacza odpowiadać na jakieś pytanie względem modelu graficznego. Bardziej formalnie, oznacza estymować jakąś właściwość statystyczną nieznanej zmiennej losowej na podstawie innych znanych albo zaobserwowanych zmiennych. Najpopularniejsze estymowane właściwości podczas “inference”:

Marginal distribution
Maximum a posteriori inference Znaczna część pytań jest NP-trudna, a trudność ta zależy od tego jak wygląda graf prawdopodobieństw.

Variable Elimination Algorithm

Quartz 4

Explorer

Bayesian Network

Niezależność w grafie (źródło: CS 228 - Probabilistic Graphical Models)

Inference w Graphical Models (źródła: CS 228 - Probabilistic Graphical Models, A visual introduction to Gaussian Belief Propagation)

Graph View

Table of Contents

Backlinks