Mnożniki Lagrangre'a

Po co?

Metoda, która pozwala rozwiązać zadanie optymalizacyjne:

$\min f(x,y)$ przy ograniczeniu $g(x,y)=k$. Zauważ, że w tym problemie ograniczeniem jest równanie (nie może być nierówność)!

Rozwiązanie

Najpierw przyjrzyjmy się funkcji 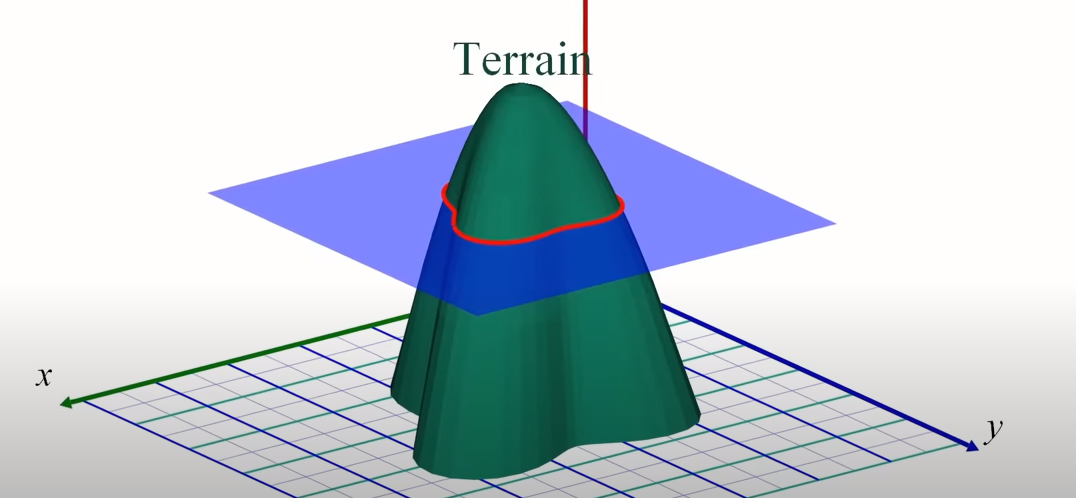$g$: Funkcję $g$ przecinamy płaszczyzną równoległą do xy - czerwona linia to poziomica (ang. level curve). Naszym przyjętym ograniczeniem jest to, że $x$ oraz $y$ muszą leżeć właśnie na tej czerwonej linii.

Fakt

Gradient funkcji $g$ na poziomicy w dowolnym punkcie jest zawsze prostopadły do poziomicy w tym punkcie:

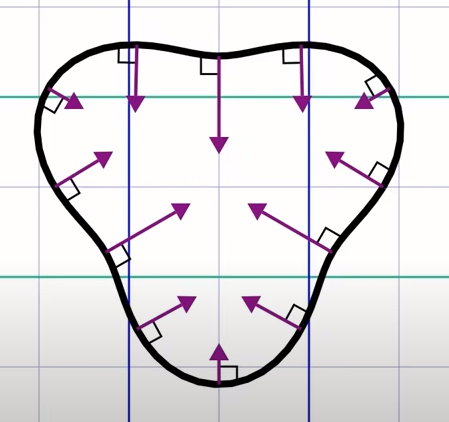
No więc teraz można sobie wyobrazić taką funkcję 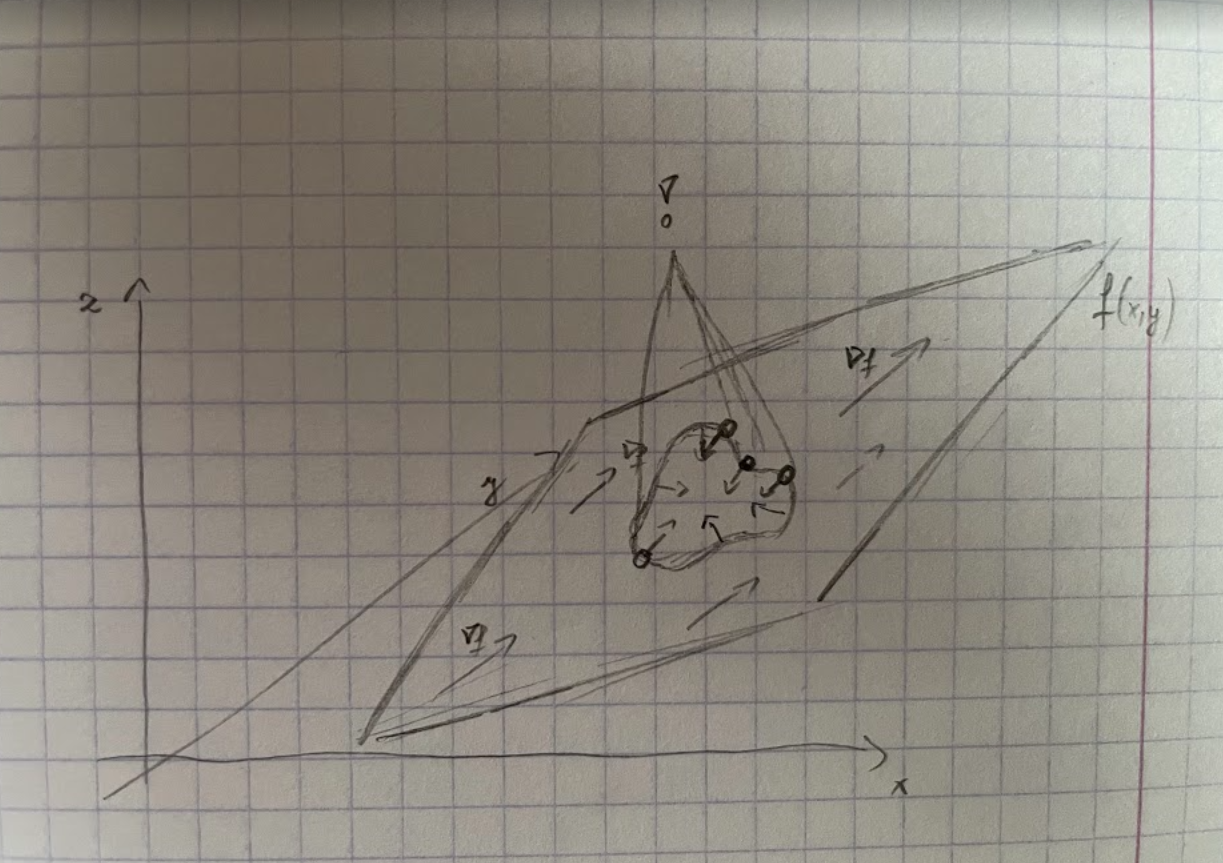$f$: Optymalizując funkcję $f$, możemy się poruszać tylko po linii wskazywanej przez ograniczenie $g$. Punkty podejrzane o maksimum lub minimum to te punkty zaznaczone kółeczkami na powyższym obrazku. W tych punktach, jeśli przesuniemy się w prawo lub w lewo po linii ograniczającej ($g$) to dojdziemy do mniejszej wartości funkcji $f$, więc są to lokalne minima (maksima). Zauważmy, że w tych punktach gradient $g$ jest równoległy do gradientu $f$! Jest to kluczowa obserwacja. Wniosek jest taki, że w tych punktach $\nabla f=\lambda \nabla g$.

Musimy więc rozwiązać układ równań: $\{\begin{array}{l}\nabla f=\lambda \nabla g\\ g(x,y)=k\end{array}$ gdzie $\lambda$ nazywane jest mnożnikiem Lagrange’a.

Źródło: https://youtu.be/5A39Ht9Wcu0